Cấu trúc dữ liệu và giải thuật
Giải thuật chia để trị (divide and conquer)
Giải thuật chia để trị (Divide and Conquer) là gì?
Phương pháp chia để trị (Divide and Conquer) là một phương pháp quan trọng trong việc thiết kế các giải thuật. Ý tưởng của phương pháp này khá đơn giản và rất dễ hiểu: Khi cần giải quyết một bài toán, ta sẽ tiến hành chia bài toán đó thành các bài toán con nhỏ hơn. Tiếp tục chia cho đến khi các bài toán nhỏ này không thể chia thêm nữa, khi đó ta sẽ giải quyết các bài toán nhỏ nhất này và cuối cùng kết hợp giải pháp của tất cả các bài toán nhỏ để tìm ra giải pháp của bài toán ban đầu.
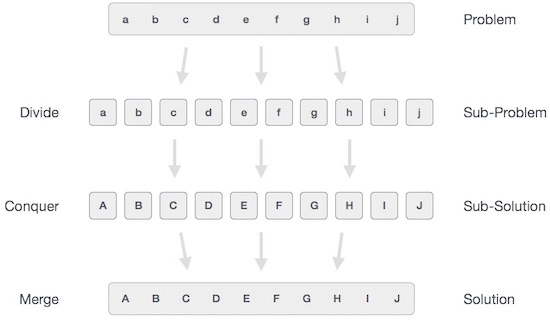
Nói chung, bạn có thể hiểu giải thuật chia để trị (Divide and Conquer) qua 3 tiến trình sau:
Tiến trình 1: Chia nhỏ (Divide/Break)
Trong bước này, chúng ta chia bài toán ban đầu thành các bài toán con. Mỗi bài toán con nên là một phần của bài toán ban đầu. Nói chung, bước này sử dụng phương pháp đệ qui để chia nhỏ các bài toán cho đến khi không thể chia thêm nữa. Khi đó, các bài toán con được gọi là “atomic – nguyên tử”, nhưng chúng vẫn biểu diễn một phần nào đó của bài toán ban đầu.
Tiến trình 2: Giải bài toán con (Conquer/Solve)
Trong bước này, các bài toán con được giải.
Tiến trình 3: Kết hợp lời giải (Merge/Combine)
Sau khi các bài toán con đã được giải, trong bước này chúng ta sẽ kết hợp chúng một cách đệ qui để tìm ra giải pháp cho bài toán ban đầu.
Hạn chế của giải thuật chia để trị (Devide and Conquer)
Giải thuật chia để trị tồn tại hai hạn chế, đó là:
Làm thế nào để chia tách bài toán một cách hợp lý thành các bài toán con, bởi vì nếu các bài toán con được giải quyết bằng các thuật toán khác nhau thì sẽ rất phức tạp.
Việc kết hợp lời giải các bài toán con được thực hiện như thế nào.
Ví dụ giải thuật chia để trị
Dưới đây là một số giải thuật được xây dựng dựa trên phương pháp chia để trị (Divide and Conquer):
- Giải thuật sắp xếp trộn (Merge Sort)
- Giải thuật sắp xếp nhanh (Quick Sort)
- Giải thuật tìm kiếm nhị phân (Binary Search)
- Nhân ma trận của Strassen

25 Th3 2021
24 Th3 2021
29 Th3 2021
25 Th3 2021
24 Th3 2021
25 Th3 2021